1. Tree sort
Tree sort adalah metode sorting dengan cara membangun pohon biner dengan
menampilkan 3 hasik output: PreOrder,InOrder,PostOrder.
Konsep dan Algoritma:
Konsep dasar dari tree sort adalah sebagaimana sebuah pohon, ada akar,
batang, ranting, daun, dsb. Dalam tree sort ada istilah akar atau root dan daun
atau leaf.
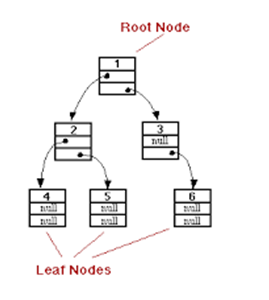
Perhatikan gambar di bawah ini.
Ketentuan dari gambar diatas adalah :
1. menjadi akar ,
2. menjadi subtree kiri,
3. menjadi subtree kanan,
4 & 5. menjadi daun dari subtree kiri ,
6. menjadi daun dari subtree kanan.
Setiap objek dalam pohon biner berisi dua
pointer, biasanya disebut kiri dan kanan.Selain pointer ini tentu saja node
dapat berisi tipe data lainnya. Misalnya, pohon biner integer bisa terdiri dari
objek dari jenis berikut:
struct Node {
int item; / /
Data dalam node ini.
Node *kiri; / / Pointer ke subtree
kiri.
Node * kanan; / / Pointer ke
subtree kanan.
}
Program tree sort :
#include<stdio.h>
#include<conio.h>
#include<malloc.h>
typedef struct
node{
int data;
node *left;
node *right;
};
node *root=NULL;
void
Tambahnode(node **root, int isi) {
if((*root)==NULL){
node *baru;
baru= new node;
baru->data = isi;
baru->left = NULL;
baru->right = NULL;
(*root)=baru;
}
}
void preorder(node
*root) {
if(root !=NULL) {
printf(“%i, “, root->data);
preorder(root->left);
preorder(root->right);
}
}
void inorder(node
*root) {
if(root !=NULL) {
inorder(root->left);
printf(“%i, “, root->data);
inorder(root->right);
}
}
void
postorder(node *root) {
if(root !=NULL) {
postorder(root->left);
postorder(root->right);
printf(“%i, “, root->data);
}
}
int main(){
int nil;
int x;
int y;
x=40;y=3;
gotoxy(x,y);
printf(“100\n”);
gotoxy(x-10,y+1);
printf(“90″);
gotoxy(x+10,y+1);
printf(“200\n”);
gotoxy(x-20,y+2);
printf(“80″);
gotoxy(x+20,y+2);
printf(“300\n”);
gotoxy(x-30,y+3);
printf(“70″);
gotoxy(x+30,y+3);
printf(“400\n”);
Tambahnode(&root,nil=100);
Tambahnode(&root->left,nil=90);
Tambahnode(&root->left->left,nil=80);
Tambahnode(&root->left->left->left,nil=70);
Tambahnode(&root->right,nil=200);
Tambahnode(&root->right->right,nil=300);
Tambahnode(&root->right->right->right,nil=400);
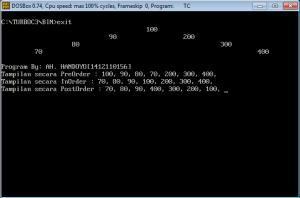
printf(“\nProgram By: AH. HANDOYO[1412110156]”);
printf(“\nTampilan secara PreOrder : “);
preorder(root);
printf(“\nTampilan secara InOrder : “);
inorder(root);
printf(“\nTampilan secara PostOrder : “);
postorder(root);
}
Output Program :
2. Selection sort
Algoritma sorting sederhana yang lain adalahSelection Sort. Ide dasarnya adalah melakukan beberapa kali pass untuk melakukan penyeleksianelemen struktur data. Untuk sorting ascending(menaik), elemen yang paling kecil di antara elemen – elemenyang belum urut, disimpan indeksnya, kemudian dilakukan pertukaran nilai elemen denganindeks yang disimpan tersebut dengan elemen yangpaling depan yang belum urut. Sebaliknya, untuksorting descending (menurun), elemen yang paling. besar yang disimpan indeksnya kemudian ditukar.
Algoritma selection sort dapat dirangkum sebagaiberikut:
1. Temukan nilai yang paling minimum (atau sesuaikeinginan) di dalam struktur data. Jika ascending, maka yang harus ditemukan adalah nilai yang paling minimum. Jika descending, maka temukan nilai yang paling maksimum.
2. Tukar nilai tersebut dengan nilai pada posisi pertama di bagian struktur data yang belum diurutkan.
3. Ulangi langkah di atas untuk bagian struktur data yang tersisa.
3. Exchange
sort
•
Sangat
mirip dengan Bubble Sort
•
Banyak
yang mengatakan Bubble Sort sama dengan Exchange Sort
•
Pebedaan
: dalam hal bagaimana membandingkan antar elemen-elemennya.
•
Exchange
sort membandingkan suatu elemen dengan elemen-elemen lainnya
dalam array tersebut, dan melakukan pertukaran elemen jika perlu. Jadi ada elemen yang selalu menjadi elemen pusat
(pivot).
•
Sedangkan
Bubble sort akan membandingkan elemen pertama/terakhir dengan elemen
sebelumnya/sesudahnya, kemudian elemen tersebut itu akan menjadi pusat
(pivot) untuk dibandingkan dengan elemen sebelumnya/sesudahnya lagi, begitu
seterusnya.
Exchange sort 2
4. Heap sort
Heap Sort adalah sebuah algoritma pengurutan
yang paling lambat dari algoritma yang memiliki kompleksitas O(n log n). Tetapi
tidak seperti algoritma Merge Sort dan Quick Sort, algoritma Heap Sort tidak
memerlukan rekursif yang besar atau menggunakan banyak tabel (array). Oleh
karena itu, Heap Sort adalah pilihan yang baik untuk sebuah kumpulan data yang
besar.
Algoritma ini bekerja dengan menentukan elemen
terbesar (atau terkecil) dari sebuah daftar elemen, dan diletakkan pada akhir
(atau awal) dari daftar tersebut. Heap sort menyelesaikan sebuah pengurutan
menggunakan struktur data yang disebut heap.
Algoritma
ini dimulai dengan membangun sebuah array heap dengan membangun tumpukan dari
kumpulan data, lalu memindahkan data terbesar ke bagian belakang dari sebuah
tabel hasil. Setelah itu, array heap dibangun kembali, kemudian mengambil
elemen terbesar untuk diletakkan di sebelah item yang telah dipindahkan tadi.
Hal ini diulang sampai array heap habis.
Jadi secara
umum, algoritma ini memerlukan dua buah tabel; satu tabel untuk menyimpan heap,
dan satu tabel lainnya untuk menyimpan hasil. Walaupun lebih lambat dari Merge
Sort atau Quick Sort, algoritma ini cocok untuk digunakan pada data yang
berukuran besar.
Penerapan Algoritma Pengurutan Heap
Sort
Salah satu contoh penerapan algoritma
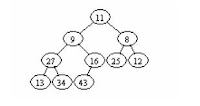
pengurutan (sorting algorithm) heap sort adalah sebagai berikut: Misalkan
terdapat suatu array bilangan bulat yang terdiri dari sepuluh buah anggota
dengan nilai data 11, 9, 8, 27, 16, 25, 12, 13, 34, dan 43. Kita akan mengurutkan
data diatas dengan menggunakan heapsort. Pertama-tama, array di atas dapat
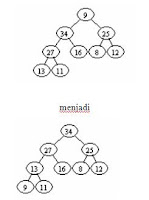
dipandang sebagai suatu Complete Binary Tree (CBT) sebagai berikut:
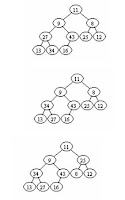
Selanjutnya algoritma metoda heapify
dilakukan dengan iterasi dari subtree node ke-4, ke-3, dan seterusnya
berturut-turut hingga mencapai root (akar). Iterasi dilakukan mulai dari node
ke-4 karena N/2 dalam contoh di atas adalah 5. Dan elemen kelima dari array
memiliki nilai indeks 4 sebab indeks array biasanya diawali dari 0. Penerapan
algoritma metoda heapify terhadap Complete Binary Tree (CBT) pada contoh di
atas menghasilkan operasi-operasi pertukaran sebagai berikut:
1. Subtree
node ke-4: pertukaran 16 dengan 43
2. Subtree
node ke-3: pertukaran 27 dengan 34
3. Subtree
node ke-2: pertukaran 8 dengan 25
4. Subtree
node ke-1: pertukaran 9 dengan 43, lalu pertukaran 9 dengan 16
5. Subtree
node ke-0: pertukaran 11 dengan 43, lalu pertukaran 11 dengan 34, serta
akhirnya pertukaran 11 dengan 27 Perubahan-perubahan (pertukaran) tersebut
dapat digambarkan sebagai berikut:
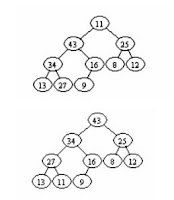
Semua perubahan di atas terjadi dalam array
yang bersangkutan, sehingga pada akhirnya diperoleh tree terakhir yang
merupakan heap tree. Sementara itu, dalam iterasi yang melakukan/menerapkan
algoritma metoda remove( ) dan algoritma metoda reheapify() akan terjadi
pemrosesan berikut:
1. Setelah
43 di-remove dan 9 menggantikan posisi yang ditinggalkan oleh 43, maka terjadi
reheapify: penukaran 9 dengan 34, 9 dengan 27, dan 9 dengan 13.
 dan data yang telah terurut adalah
43.
dan data yang telah terurut adalah
43.
2. Setelah
34 di-remove dan 11 menggantikan posisi yang ditinggalkan oleh 34, maka terjadi
reheapify: penukaran 11 dengan 27, dan 11 dengan 16.
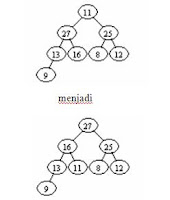 dan data yang telah terurut adalah
34, 43.
dan data yang telah terurut adalah
34, 43.
3. Setelah 27 di-remove dan 9 menggantikan posisi yang ditinggalkan oleh 27,
maka terjadi reheapify: penukaran 9 dengan 25, dan 9 dengan 12.
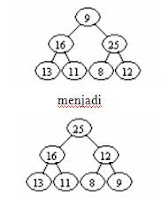 dan data yang telah terurut adalah
27, 34, 43.
dan data yang telah terurut adalah
27, 34, 43.
4. Demikian seterusnya dilakukan
algoritma metoda remove dan algoritma metoda reheapify hingga tidak ada lagi
node yang tersisa. Dan pada akhirnya akan didapatkan hasil data yang telah
terurut adalah 8, 9, 11, 12, 13, 16, 25, 27, 34, 43.
Program Heap
Sort & Penjelasannya
<#include <>
void restoreHup(int*,int); // pemanggilan fungsi
void restoreHup
void restoreHdown(int*,int,int); //pemanggilan
fungsi void restoreHdown
void main()
{ // pembuka void main
int a[20],n,i,j,k; // mendeklarasikan bahwa a[20]
,n,i,j,k adalah integer
printf(" Masukkan jumlah element : ");//
untuk menampilkan kelayar perintah memasukkan jumlah element
scanf("%d",&n); // untuk
mengidentifikasikan nilai yang dimasukkan melalui keyboard
printf(" Masukkan element : "); //untuk
menampilkan kelayar perintah untuk memasukkan element
for(i=1;i<=n;i++) //funsi for dimana jika
ketentuan untuk i terpenuhi maka progran di bawahnya akan dijalankan
{ // pembuka fungsi for
scanf("%d",&a[i]); // untuk
mengidentifikasi array a
restoreHup(a,i); // a , i dalam fungsi restoreHup
} // penutup fungsi for
j=n; // nilai j sama dengan n
for(i=1;i<=j;i++) //funsi for dimana jika
ketentuan untuk i terpenuhi maka progran di bawahnya akan dijalankan
{ // pembuka fungsi for
int temp; // temp sebagai integer
temp=a[1]; // temp sama dengan nilai array a yang
pertama
a[1]=a[n]; // nilai array a yg ke 1 sama dengan
array a yang ke n
a[n]=temp; // nilai array a yang ke n sama dengan
nilay temp
n--; // nilai n selalu berkurang 1
restoreHdown(a,1,n); // a , 1, n dalam fungsi
restoreHdown
} // penutup fungsi for
n=j; // n sama dengan nilai j
printf(" Here is it... "); // untuk
menampilkan perintah ke dalam layar
for(i=1;i<=n;i++) //funsi for dimana jika
ketentuan untuk i terpenuhi maka progran di bawahnya akan dijalankan
printf("%4d",a[i]); // untuk menampilkan
nilai array ke i ke layar
} // penutup void main
void restoreHup(int *a,int i) // fungsi void
restore Hup
{ // pembuka fungsi foid restoreHup
int v=a[i]; // v sama dengan nilai array a yang
ke i
while((i>1)&&(a[i/2]
{ // pembuka fungsi while
a[i]=a[i/2]; // nilai array a yang ke i sama
dengan nilai array a yang ke i/2
i=i/2; // nilai i sama dengan nilai i/2
} //penutup fungsi while
a[i]=v; // nilai array a yang ke i sama dengan
nilai v
} // penutup fungsi while
void restoreHdown(int *a,int i,int n) // fungsi
void restoreHdown
{ // pembuka fungsi void restoreHdown
int v=a[i]; // v sama dengan nilai array a yang
ke i sebagai integer
int j=i*2;// nilai j sama dengan i kali 2 ialah
integer
while(j<=n) // fungsi while akan dijalankan
bila ketentuannya terpenuhi
{ // pembuka fungsi while
if((j
j++; // nilai j akan selalu tambah 1
if(a[j]
break;
a[j/2]=a[j]; // nilai array a yang ke j/2 sama
dengan nilai array a yang ke j
j=j*2; // nilai j sama dengan nilai j*2
}// penutup fungsi while
a[j/2]=v;// nilai array a yang ke j/2 sama dengan v
}// penutup fungsi void restorehdown
//Suatu program untuk mengimplementasikan Heap
Sort>
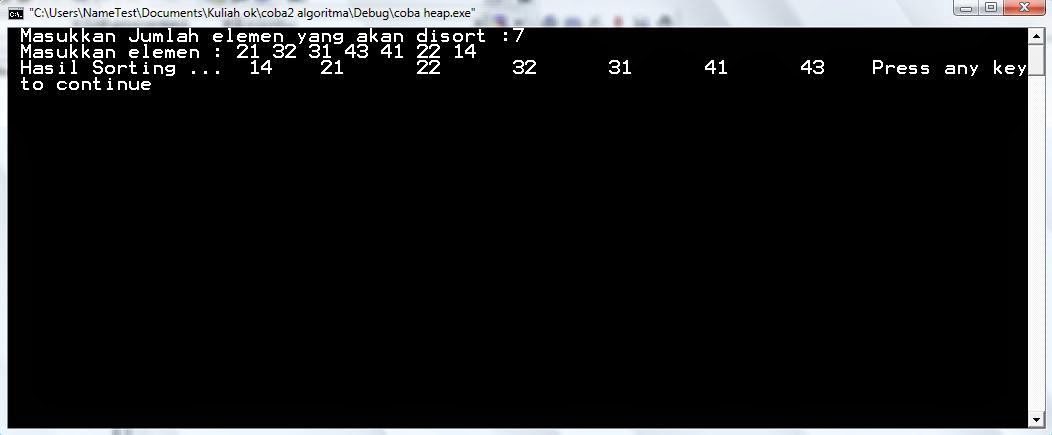
Hasil
Program diatas :
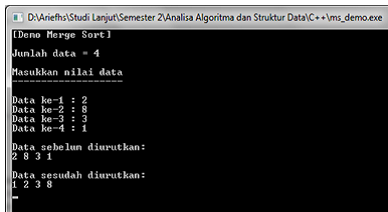
5. Marge sort
Algoritma Merge Sort ditemukan oleh John vonNeumann di tahun 1945. Merge Sort termasuk paradigma algoritma divide and conquer (kurang lebihberarti: bagi dan atasi). Hal ini dikarenakan algoritma ini melakukan pembagian struktur data sebelumkemudian dioperasi satu per satu. Intinya, algoritma ini menggunakan dua ide utama sebagai berikut :
1. Sebuah list yang kecil membutuhkan langkahyang lebih sedikit untuk pengurutan daripadasebuah list yang besar.
2. Untuk membentuk sebuah list terurut dari duabuah list terurut membutuhkan langkah yanglebih sedikit daripada membentuk sebuah listterurut dari dua buah list tak terurut. Contoh: hanya diperlukan satu kali traversal untukmasing-masing list jika keduanya sudah terurut.
Algoritma Merge Sort sederhananya, dapat ditulis berikut:
1. Bagi list yang tak terurut menjadi dua samapanjang atau salah satunyalebih panjang satu elemen.
2. Bagi masing-masing dari 2 sub-list secara rekursif sampai didapatkan list dengan ukuran 1.
3. Gabung 2 sublist kembali menjadi satu list terurut.
Algoritma :
Algoritma Merge sort sebenarnya sederhana[9]: bagi larik menjadi dua sama besar, urutkan bagian pertama, urutkan bagian kedua, lalu gabungkan.
Sebagai contoh, jika terdapat data berupa 38, 27, 43, 3, 9,82, dan 10 maka ilustrasi pengurutannya adalah sebagai berikut:
Pseudocodeuntuk merge sort[6] adalah sebagai berikut:
mergesort(data)
if data memiliki setidaknya dua
elemen
mergesort (separuh kiri dari data);
mergesort (separuh kanan dari data ;
merge (kedua bagian ke dalam suatu urutan);
Sedangkan pseudocodeuntuk merge itu sendiri adalah:
merge (arrayl, pertama, terakhir)
tengah = (pertama + terakhir) / 2;
il = 0;
i2 = pertama;
i3 = tengah + 1;
while kedua sub larik dari array1 memiliki elemen
if arrayl[i2] < arrayl[i3]
temp[il++] = arrayl[i2++];
else
temp[il++] = arrayl[i3++];
masukkan ke dalam temp sisa elemen dari arrayl;
masukkan ke arrayl isi dari temp;
Contoh program merge sort :
void merge(int kiri,int tengah, int kanan)
{
int h,i,j,b[50],k;
h=kiri;
i=kiri;
j=tengah+1;
while((h<=tengah)&&
(j<=kanan))
{
if(bilangan[h]<=
bilangan[j])
{
b[i]=bilangan[h];
h++;
}
else
{
b[i]=bilangan[j];
j++;
}
i++;
}
if(h>tengah)
{
for(k=j;k<=kanan;k++)
{
b[i]=bilangan[k];
i++;
}
}
else
{
for(k=h;k<=tengah;k++)
{
b[i]=bilangan[k];
i++;
}
}
else
{
for(k=h;k<=tengah;k++)
{
b[i]=bilangan[k];
i++;
}
}
for(k=kiri;k<=kanan;k++)
bilangan[k]=b[k];
}
void merge_sort(int kiri,
int kanan)
{
int tengah;
if(kiri<kanan)
{
tengah=(kiri+kanan)/2;
merge_sort(kiri,tengah);
merge_sort(tengah+1,
kanan);
merge(kiri,tengah,
kanan);
}
}
Output program :
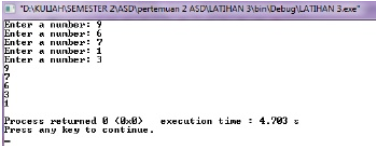
6. Shell sort
Metode ini dikembangkan oleh Donald L. Shell pada
tahun 1959. Dalam metode ini jarak antara dua elemen yang dibandingkan
dan ditukarkan tertentu. Secara singkat metode ini dijelaskan sebagai berikut.
Pada langkah pertama, kita ambil elemen pertama dan kita bandingkan dan
kita bandingkan dengan elemen pada jarak tertentu dari elemen pertama tersebut.
Kemudain elemen kedua kita bandingkan dengan elemen lain dengan jarak yang sama
seperti jarak yang sama seperti diatas. Demikianseterusnya sampai seluruh
elemen dibandingkan. Pada langkah kedua proses diulang dengan langkah yang
lebih kecil, pada langkah ketiga jarak tersebut diperkecil lagi seluruh proses
dihentikan jika jarak sudah sama dengan satu.
Contoh dari proses Sorting dengan menggunakan metode Shell Sort :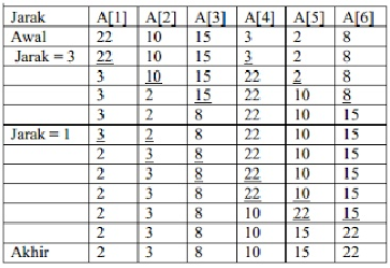
Program Shell Sort sebagai berikut :
/*shell sort*/
#include<iostream>
using namespace std;
int main(void)
{
int
array[5]; // An array of integer
int length = 5; // Length of
the array
int i, j, d;
int tmp, flag;
//some input
for(i=0; i<length; i++)
{
cout<<"Enter
a number: ";
cin>>array[i];
}
//Algorithm
d=length;
flag=1;
while(flag || (d>1))
{
flag=0;
d=(d+1)/2;
for(i=0; i<(length -d);
i++)
{
if(array[i+d]>array[i])
{
tmp=array[i+d];
array[i+d]=array[i];
array[i]=tmp;
flag=1;
}
}
}
//Some output
for(i=0; i<5; i++)
{ cout<<array[i]<<endl;
}
}
Output program :
Algoritma
1. Mula
2. Membaca
file header.
3. Membaca
fungsi main
4. Membaca
fungsi array yang didalamnya terdpat fungsi panjang.
5. Membaca
perulangan.
6. Membaca
percabangan.
7. Membaca
fungsi temp.
8. Membaca
perulangan.
9. Pemanggilan
array[i].
10. Cetak
hasil.
11. Selesai.
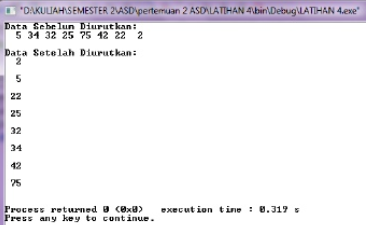
77. Quick sort
Quick Sort adalah algoritma sorting yang terkenal yang dirancang oleh C.A.R. Hoare pada tahun 1960 ketika bekerja untuk perusahaan manufaktur komputer saintifik kecil, Elliott Brothers. Algoritma ini rekursif, dan termasuk paradigma algoritma divide and conquer.
Algoritma Quick Sort ini terdiri dari 4 langkah utama:
1.) Jika struktur data terdiri dari 1 atau 0 elemen yang harus diurutkan, kembalikan struktur data itu apa adanya.
2.) Ambil sebuah elemen yang akan digunakansebagai pivot point (poin poros). (Biasanyaelemen yang paling kiri.)
3.) Bagi struktur data menjadi dua bagian satudengan elemen-elemen yang lebih besar daripada pivot point, dan yang lainnya denganelemen-elemen yang lebih kecil dari pada pivot point. 4.
4.) Ulangi algoritma secara rekursif terhadapkedua paruh struktur data.
Contoh Program Quick Sort :
#include<iostream.h>
#include<iomanip.h>
void quickSort(int[], int);
void q_sort(int[], int, int);
void main()
{
int NumList[8]={5,34,32,25,75,42,22,2};
int temp;
cout<<"Data Sebelum Diurutkan: \n";
for(int d=0; d<8; d++)
{
cout<<setw(3)<<NumList(d);
}
cout<<"\n\n";
quickSort (NumList,8);
cout<<"Data Setelah Diurutkan: \n";
for (int iii=0; iii<8; iii++)
cout<<"setw(3)"<<NumList[iii]<<endl<<endl;
}
void quickSort(int numbers[], int array_size)
{
q_sort(number, 0, array_size-1);
}
void q_sort(int number[], int left, int right)
{
int pivot, l_hold, r_hold;
l_hold=left;
r_hold=right;
pivot = numbers[left];
while (left<right)
{
while((numbers[right]>=pivot || (left<right))
right--;
if(left != right)
{
numbers[left]=numbers[right];
left++;
}
while ((numbers[left] <=pivot) && (left<right))
left++;
if (left != right)
{
number[right]=numbers[left];
right--;
}
}
numbers[left]=pivot;
pivot=left;
left=l_hold;
right=r_hold;
if (left<pivot)
q_sort(numbers, left, pivot-1);
if (right>pivot)
q_sort(numbers, pivot+1, right);
}
Script program yang benar :
/*Quick Sort*/
#include<iostream>
#include<iomanip>
#include <conio.h>
using namespace std;
void quickSort(int[], int);
void q_sort(int[], int, int);
int main()
{
int NumList[8]={5,34,32,25,75,42,22,2};
int temp;
cout<<"Data Sebelum Diurutkan: \n";
for(int d=0; d<8; d++)
{
cout<<setw(3)<<NumList[d];
}
cout<<"\n\n";
quickSort (NumList,8);
cout<<"Data Setelah Diurutkan: \n"; for (int iii=0; iii<8; iii++) cout<<setw(3)<<NumList[iii]<<endl<<endl;
}
void quickSort(int numbers[], int array_size)
{
q_sort(numbers, 0, array_size-1);
}
void q_sort(int numbers[], int left, int right)
{
int pivot, l_hold, r_hold;
l_hold=left;
r_hold=right;
pivot = numbers[left];
while (left<right)
{
while((numbers[right]>=pivot) &&(left<right))
right--;
if(left != right)
{
numbers[left]=numbers[right];
left++;
}
while ((numbers[left] <=pivot) && (left<right))
left++;
if (left != right)
{
numbers[right]=numbers[left];
right--;
}
}
numbers[left]=pivot;
pivot=left;
left=l_hold;
right=r_hold;
if (left<pivot)
q_sort(numbers, left, pivot-1);
if (right>pivot)
q_sort(numbers, pivot+1, right);
}
Output Program :